The raw materials are high-purity Cr₂O₃ (Huawei Ruike Chemical Co., Ltd., Beijing, China), Ta₂O₅ (Huawei Ruike Chemical Co., Ltd., Beijing, China) and Nb₂O₅ (Macklin Biochemical Technology Co., Ltd., Shanghai, China) powders. The materials were mixed according to the nominal composition of CrTa_0.5Nb_0.5O₄ with deionized water and zirconia balls in a mass ratio of 1:2:6 and then ball milled for 12 h at 120 rpm. After drying in an oven, the mixture was sieved through a 300 -mesh screen to achieve the desired powder fineness. Subsequently, the powder underwent preparation in an air atmosphere at the temperature of 1150^∘C with a holding time of 2 h according to reaction (1):

These parameters were selected because both CrTaO₄ and CrNbO₄ powders were synthesized at 1150^∘C for 2 h. The phase composition of the as-synthesized CrTa_0.5Nb_0.5O₄ powders was examined by an X-ray diffractometer (XRD, Rigaku Ultima IV, Japan) using CuK αradiation (λ=1.5406Å ) with a step size of 0.02^∘ at a scanning rate of 1^∘/min. The microstructure and particle size distribution were analyzed in a scanning electron microscope (SEM, JSM-7001F, Japan). In addition, the crystal structure of CrTa_0.5Nb_0.5O₄ was refined by the Rietveld method (Reflex code, Materials Studio program, Accelrys Inc., San Diego, USA). After that, the synthesized pure-phase CrTa_0.5Nb_0.5O₄ powders were ground and screened to obtain particles with uniform size, which is beneficial to the preparation of subsequent dense bulk.

Bulk CrTa_0.5Nb_0.5O₄ was prepared by the hot-press sintering method (in a ZT-50-22Y hot-pressing furnace, Shanghai Chenhua Science and Technology Co., Ltd, China). Through monitoring the displacement-temperature-time curve during the hot-pressing process, the optimal processing parameters for fabricating bulk CrTa_0.5Nb_0.5O₄ were determined as follows: CrTa_0.5Nb_0.5O₄ powders were loaded into a graphite mold with a diameter of 50 mm, heated to 1400^∘C at a rate of 10^∘C/min, maintained at 30 MPa for 40 min, cooled to 800^∘C at a rate of 5^∘C/min, and then furnace-cooled to room temperature. After cooling, the surface contaminants were removed using a grinding machine. The final density of the bulk CrTa_0.5Nb_0.5O₄ was measured by the Archimedes method. The theoretical density of CrTa_0.5Nb_0.5O₄ was calculated from the mass of the atoms in a unit cell and the cell dimensions obtained by the Rietveld refinement of XRD data. Phase identification in the bulk sample was conducted by XRD at a scanning rate of 1^∘/min. The microstructure and grain size distribution of the bulk CrTa_0.5Nb_0.5O₄ were observed in a scanning electron microscope (SEM, JSM-7001F, Japan). For in-depth and detailed microstructure analysis, atomic-resolution high-annular dark field (HAADF) and annular bright field (ABF) scanning transmission electron microscopy (STEM) analyses were carried out in a Thermo Fisher Spectra 300 aberration-corrected transmission electron microscope.

The Young's modulus (E ) and shear modulus (G ) of the bulk CrTa_0.5Nb_0.5O₄ were measured using a rectangular bar with the size of 3 mm×15 mm×40 mm by employing the impulse excited resonance method (DST-V, China National Inspection and Testing Group Co., Ltd). According to the China National Building Materials Industry Standard (JC/T 2172-2013) [15], the E and G were calculated based on the obtained flexural resonate frequency and torsional resonate frequency respectively:

In these equations, β and γ were calculated using the following Eqs. (4) and (5):

where E and G are Young's modulus and shear modulus in Pa, respectively; m is the mass of rectangular bar in kg;f_F and f_T are the fundamental flexural resonant frequency and torsional resonate frequency in Hz, respectively; b,L, and t are the width, length, and thickness of the rectangular bar in m, respectively; β is the shape parameter, and γ is the empirical correction parameter. The bulk modulus (B ) and Poisson's ratio (v ) were calculated from the E and G according to the following relationships [16]:

Vickers hardness (H_v ) was measured by a microhardness tester (HXD-1000TMC/LCD, Shanghai Taiming, China) at loads of 0.98, 1.96, 2.94,4.90, and 9.80 N, with a dwell time of 15 s. Seven measurement points were taken under each load, and the hardness value at the corresponding load was obtained by calculating the average of these seven points. The morphology of the indentation was observed by a scanning electron microscope (SEM, JSM-7001F, Japan). The H_V was calculated according to Eq. (8):

where P is the load, S is the surface area of the indentation, θ is the angle between opposite face of the intender, and d is the diagonal length of the indentation.

Flexural strength (σ_f ) was measured by the three-point bending method with a span of 30 mm and a crosshead speed of 0.5 mm/min. Samples were cut into the size of 3 mm×4 mm×40 mm and were polished and chamfered with a polishing lap. The flexural strength was calculated by using Eq. (9) [17]:

where F is the load, l is the length of the span, b is the width, and h is the thickness of the sample. Fracture toughness (K_IC ) was measured using single-edge V-notched beam specimens (SEVNB) in three-point bending. The V-notches with a sharp tip radius of ca.8μ m and notch depth of ca. 860μ m were cut at the center of the 3 mm×40 mm surfaces of the rectangular samples by automated means with a razor blade coated with diamond paste before testing. The fracture toughness was calculated by using Eqs. (10), (11) and (12) [18]:

where d is the depth of V-notches; w and h represent the width and height of the sample, respectively; Y is a stress intensity shape factor; P_max  is the maximum force at which fracture occurred; S_O and S_i are the outer and inner span, respectively.

The melting point of CrTa_0.5Nb_0.5O₄ was measured by directly observing the shape and volume changes during the laser heating process in a system developed at Shanghai Institute of Ceramics, Chinese Academy of Sciences. The bulk sample was placed in a graphite crucible positioned at the center of a vacuum chamber. The graphite crucible was heated by four symmetrically arranged laser beams, and the temperature was measured using an infrared pyrometer. The shape and volume of the sample were monitored via an optical system. When the collapse of the solid sample was observed, the corresponding temperature (melting point) at that moment was recorded.

The average thermal expansion coefficient (TEC) of CrTa_0.5Nb_0.5O₄ was measured by an optical dilatometer (Misura ODHT 1600-50, Expert System Solutions, Italy). The test specimen is a rectangular bar with the dimension of 3 mm in thickness, 4 mm in width, and 15 mm in length (height). A 45^∘ sharp edge was cut on top end of the height of the test specimen. Temperature dependent change in the length of the specimen from room temperature to 1473 K was recorded continuously by a personal computer. The heating rate during testing was controlled at 5^∘C/min. The average linear TEC of CrTa_0.5Nb_0.5O₄ was calculated according to Eq. (13):

where α is the average linear TEC, L is the length of the sample, T is the temperature.

Thermal diffusivity (D_th  ) of CrTa_0.5Nb_0.5O₄ was determined by laser flash method (LFA457, NETZSCH, Germany). A specimen with the dimension of $\mathrm{\Phi }10\text{ }\mathrm{m}\mathrm{m}\times 2\text{ }\mathrm{m}\mathrm{m}$ was used for the test. Before thermal diffusivity measurement, the front and back faces of the specimen were sprayed with two layers of carbon to minimize the radiative heat transport through the specimen. The heat capacity was obtained from the data of its constituent oxides according to Neumann-Kopp rule [19]. The thermal conductivity of CrTa_0.5Nb_0.5O₄ was calculated according to the following equation [20]:

where k is the thermal conductivity, D_th  is the thermal diffusivity, C_p is the heat capacity, and ρ(T) is the temperature dependent density, which can be calculated using the TEC.

In Fig. 1(a), the experimental XRD pattern of CrTa_0.5Nb_0.5O₄ powder, synthesized by calcining the Cr₂O₃,Nb₂O₅ and Ta₂O₅ powder mixture at 1150^∘C for 2 h in an air atmosphere, was compared with the theoretical XRD pattern generated using the Reflex code in the Accelrys Materials Studio program (Accelrys Inc., San Diego, USA). Apparently, both the positions and intensities of the diffraction peaks are consistent with the calculated XRD pattern, and no extra diffraction peaks are detected. Based on these facts, we preliminarily believe that phase pure CrTa_0.5Nb_0.5O₄ powder has been successfully obtained. Since CrTa_0.5Nb_0.5O₄ can be regarded as a solid solution of CrTaO₄ and CrNbO₄, in Fig. 1(b), we compared the experimental XRD patterns of these three materials. Judging from the intensities of the diffraction peaks, the intensity of the solid solution CrTa_0.5Nb_0.5O₄ is between those of CrTaO₄ and CrNbO₄ (see the color difference in the figure). After magnifying the (110) peak, Fig. 1(c) is obtained. It is of note that the position of the diffraction peak of the solid solution CrTa_0.5Nb_0.5O₄ is also in between the two-end member CrTaO₄ and CrNbO₄. Therefore, we can assume that a new solid solution CrTa_0.5Nb_0.5O₄ has indeed been formed after calcining the Cr₂O₃,Nb₂O₅ and Ta₂O₅ powder mixture at 1150^∘C for 2 h. To further confirm that the synthesized powder is CrTa_0.5Nb_0.5O₄ and obtain the corresponding crystal structure information, Rietveld refinement was performed using Pseudo-Voigt peak shape profile, and the resultant data are presented in Fig. 1(d). The reliability factors R_p and R_wp were calculated by Eqs. (15) and (16) [21,22]:

where c is the optimization constant scaling factor, I^exp(2θ_i) is the intensity of the measured experimental spectrum, Y^back (2θ_i) is the background intensity of the measured spectrum, Y^sim(2θ_i) is the simulated diffraction intensity without the background contribution and w_i is a weighting function. The reliability factors are R_p=5.34% and R_wp=7.77%, which indicate that the Rietveld refinement results are reliable. Rietveld refinement provides the corresponding unit cell parameters and atomic position information, as shown in Table 1. Moreover, the crystal structure information of CrTaO₄ and CrNbO₄ is also presented in the table. The unit cell parameters of the refined CrTa_0.5Nb_0.5O₄ are between those of CrTaO₄ and CrNbO₄, consistent with the results in Fig. 1(c), which further confirm that the obtained powder is the solid solution CrTa_0.5Nb_0.5O₄. Fig. 1(e) shows the SEM image of CrTa_0.5Nb_0.5O₄ powders synthesized at 1150^∘C for 2 h. The ImageJ software was utilized to calculate the particle size distribution presented in Fig. 1(f). The results demonstrate that the particle size distribution range of CrTa_0.5Nb_0.5O₄ powders is relatively narrow, with an average particle size of 0.74μ m, which is conducive to the subsequent preparation of dense bulk materials.

To investigate the mechanical and thermal properties of CrTa_0.5Nb_0.5O₄, the preparation of dense bulk CrTa_0.5Nb_0.5O₄ compact is essential. Bulk CrTa_0.5Nb_0.5O₄ was synthesized via hot-pressing the as-synthesized powders in a graphite mold under vacuum at 1400^∘C under 30 MPa for 40 min. The phase composition of the hot-press sintered bulk was analyzed using XRD, as shown in Fig. 2(a). After hot-press sintering, the diffraction peaks of CrTa_0.5Nb_0.5O₄ showed no significant shift in position or change in intensity and they closely matched with those in the theoretically simulated XRD pattern. This indicates that the phase composition remained unchanged after hot-pressing, suggesting that CrTa_0.5Nb_0.5O₄ exhibits good thermal stability upon hot-press sintering at 1400^∘C. Notably, in contrast to our previous study on CrNbO₄ bulk synthesis-wherein trace amounts of Cr₂O₃ precipitation were detected after hot-pressing-the absence of secondary phases in CrTa_0.5Nb_0.5O₄ underscores the stabilizing effect of configurational entropy in the solid solution of CrTa_0.5Nb_0.5O₄. This phenomenon is consistent with the thermodynamic principle that increasing the entropy reduces the Gibbs free energy (ΔG=ΔH-TΔS ), thereby promoting phase homogeneity and inhibiting decomposition [23]. After confirming that the bulk material was phase-pure CrTa_0.5Nb_0.5O₄, we calculated the relative density of the bulk. By applying Archimedes' principle, it was calculated that the density of the bulk was 6.39 g/cm³, which was 98.6% of the theoretical density of ${\mathrm{C}\mathrm{r}\mathrm{T}\mathrm{a}}_{0.5}{\mathrm{N}\mathrm{b}}_{0.5}{\mathrm{O}}_{4}(6.48\text{ }\mathrm{g}/{\mathrm{c}\mathrm{m}}^{3}$ ). Fig. 2(b) presents a SEM image of the fracture surface of the bulk CrTa_0.5Nb_0.5O₄. Within the field of view of this image, neither micropores nor microcracks are observable. This microstructure feature suggests that the bulk CrTa_0.5Nb_0.5O₄ is near fully dense, which is in line with the measured density of 98.6 %. Fig. 2(c) shows the grain size distribution collected from Fig. 2(b) using the ImageJ software. It is seen that the grains are relatively small with a narrow size distribution. The average grain size is statistically determined to be 3.05±0.54μ m.

Elastic properties are important for technological and engineering applications of materials. The intrinsic hardness of a material is correlated with its bulk modulus (B ) and shear modulus (G ). The B is a measure of resistance to volume change by the applied pressure while the G is a measure of resistance to reversible deformations upon shear stress. Young's modulus (E ) is defined as the stress-to-strain ratio, characterizing the stiffness of the solid. Table 2 shows the B,G,E, Poisson's ratio (v ), Pugh's ratio G/B, Vickers hardness (H_v ), flexural strength (σ_f ), and fracture toughness (K_IC ) of CrTa_0.5Nb_0.5O₄. Additionally, it also includes those of CrTaO₄ [8] and CrNbO₄ [9] with the rutile-type crystal structure, typical ceramics Al₂O₃ [24], YSZ [10], and Cr-Ta-Nb based RHEAs [25] in the table. The E,G and B of CrTa_0.5Nb_0.5O₄ are higher than CrMoNbTaTiVZr, but much lower than those of Al₂O₃. Since CrTa_0.5Nb_0.5O₄ is a solid solution of CrTaO₄ and CrNbO₄, so we conduct a detailed comparison of these three materials. Notably, both the E and G of CrTa_0.5Nb_0.5O₄ are higher than those of CrTaO₄ and CrNbO₄, but its B is lower than that of these two materials. The bulk modulus of CrTa_0.5Nb_0.5O₄ is 3.3% lower than CrTaO₄ and 2.7% lower than CrNbO₄. A parallel trend is observed when compared with YSZ. The E and G of CrTa_0.5Nb_0.5O₄ are much higher than those of YSZ, but the bulk modulus B is slightly lower (∼0.57% ) than that of YSZ. A low bulk modulus typically indicates that a material is more prone to volume shrinkage under external pressure, which may affect its thermal properties such as the thermal expansion coefficient. Pugh's ratio (G/B ) and Poisson's ratio (ν ) serve as valuable indicators for characterizing the brittleness/ ductility and bonding type in crystalline materials. Specifically, materials are generally classified as brittle when the G/B ratio exceeds 0.571 [26] and the Poisson ratio is lower than 0.26 [27]. Conversely, materials with G/B ratios below this threshold and Poisson ratios above 0.26 are typically categorized as damage-tolerant, exhibiting enhanced resistance to fracture under stress. Using the measured elastic properties, the G/B ratio of CrTa_0.5Nb_0.5O₄ is calculated to be 0.680 (exceeding 0.571), while the ν is 0.233 (lower than 0.260). Thus, it can be concluded that CrTa_0.5Nb_0.5O₄ exhibits brittle behavior. To quantitatively compare the degree of brittleness, the Poisson's ratios and Pugh's ratios (G/B ) of the following materials are plotted in Fig. 3(a): CrMoNbTaTiVZr (0.317, 0.356) [28], CrMoNbTaTiVWZr (0.372,0.335 ), Y₂SiO₅(0.44,0.31) [29], CrTaO₄(0.59,0.254) [8], CrNbO₄(0.56,0.266) [9], YSZ (0.46, 0.3) [10], SiC (0.85, 0.16) [30], Al₂O₃ (0.65,0.22 ) [24], TaC(0.63,0.24) [12], $\mathrm{H}\mathrm{f}\mathrm{C}\left(\mathrm{0.81,0.18}\right)\left[31\right],{\mathrm{Y}\mathrm{b}}_{3}{\mathrm{A}\mathrm{l}}_{5}{\mathrm{O}}_{12}$ (0.64,0.24 ) [32], YbAlO₃(0.496,0.287) [33], Ti₃AlC₂(0.75,0.2) [34], ${\mathrm{M}\mathrm{n}}_{2}{\mathrm{A}\mathrm{l}\mathrm{B}}_{2}\left(\mathrm{0.71,0.21}\right)\left[35\right],{\mathrm{Y}\mathrm{T}\mathrm{a}\mathrm{O}}_{4}\left(\mathrm{0.327,0.35}\right),{\mathrm{N}\mathrm{d}\mathrm{T}\mathrm{a}\mathrm{O}}_{4}\left(\mathrm{0.459,0.30}\right)\left[36\right]$. On the ground of the data in Fig. 3(a), the two Cr and Nb containing RHEAs are judged as ductile materials, whereas CrTa_0.5Nb_0.5O₄ is more brittle than its constituent end member CrTaO₄ and CrNbO₄ as well as YSZ,Y₂SiO₅, ${\mathrm{Y}\mathrm{T}\mathrm{a}\mathrm{O}}_{4},{\mathrm{N}\mathrm{d}\mathrm{T}\mathrm{a}\mathrm{O}}_{4},{\mathrm{Y}\mathrm{b}\mathrm{A}\mathrm{l}\mathrm{O}}_{3},{\mathrm{Y}\mathrm{b}}_{3}{\mathrm{A}\mathrm{l}}_{5}{\mathrm{O}}_{12}$. Notably CrTa_0.5Nb_0.5O₄ is significantly less brittle than some typical brittle ceramics, such as SiC,HfC,Ti₃AlC₂ and Mn₂AlB₂ but exhibits comparable brittleness to Al₂O₃ and TaC.

Fig. 3(b) shows the relationship between the Vickers hardness and the indentation load of CrTa_0.5Nb_0.5O₄. As the indentation load increases (from 0.98 N to 9.80 N), the hardness of CrTa_0.5Nb_0.5O₄ monotonically decreases from 19.50 to 13.01 GPa. When the load increases to 2.98 N, cracks start to appear, which is regarded as the practical hardness value of CrTa_0.5Nb_0.5O₄. As a result, the hardness of CrTa_0.5Nb_0.5O₄ is 13.01±0.20GPa (measured under a load of 2.98 N), being lower than that of YSZ (14 GPa) [10], Al₂O₃(16GPa) [24], and SiC(32GPa) [30], but higher than the two end member materials CrTaO₄(12.20±0.44) [8] and CrNbO₄(10.20±0.58) [9]. This phenomenon is primarily ascribed to solid solution strengthening, wherein the dimensional and valence electron disparities among metal atoms (Cr,Ta,Nb ) in the multi-component solid solution elicit significant lattice distortion. Such distortion hinders dislocation glide, thereby elevating the solid solution's hardness in comparison to its end member analogs. Fig. 3(c) presents the SEM morphology of an indentation generated in CrTa_0.5Nb_0.5O₄ under a load of 2.98 N. The indentation exhibits distinct boundaries, and straight cracks emanate from its four corners, which is consistent with the failure characteristics of brittle materials. A magnified view of the crack, as shown in Fig. 3(d), reveals crack deflection. This mechanism effectively mitigates the tendency toward brittle fracture under stress and enhances the material's toughness. The flexural strength of CrTa_0.5Nb_0.5O₄ is 201±12MPa, which is higher than that of CrTaO₄(142±14MPa) [8], YSZ (120 MPa ) [10], but lower than that of CrNbO₄(205±8MPa) [9] and Al₂O₃(300-400MPa) [24]. Notably, the fracture toughness of CrTa_0.5Nb_0.5O₄ is 2.07±0.017MPa⋅m¹/ ², representing a 10.7% increase over ${\mathrm{C}\mathrm{r}\mathrm{T}\mathrm{a}\mathrm{O}}_{4}\left(1.87\pm 0.074\mathrm{M}\mathrm{P}\mathrm{a}\cdot {\mathrm{m}}^{1}/{ }^{2}\right)$ and a 33.1% increase over ${\mathrm{C}\mathrm{r}\mathrm{N}\mathrm{b}\mathrm{O}}_{4}\left(1.54\pm 0.124\mathrm{M}\mathrm{P}\mathrm{a}\cdot {\mathrm{m}}^{1}/{ }^{2}\right)$, while remaining comparable to YSZ (1.7-2.0MPa⋅m¹/ ² ). The improvement in toughness can also be ascribed to the solid solution strengthening mechanism, wherein lattice distortion induced by size discrepancies among the three atoms hinders dislocation glide and retards crack propagation. At present, YSZ is the most commonly used thermal barrier coating material, in line with CrTaO₄ and CrNbO₄ the similar elastic and mechanical properties of CrTa_0.5Nb_0.5O₄ to those of YSZ give us a hint that CrTa_0.5Nb_0.5O₄ is presumably a new thermal barrier material.

CrTa_0.5Nb_0.5O₄ exhibits high hardness, flexural strength, and fracture toughness. However, for thermal barrier coating (TBC) applications, the matching of thermal expansion coefficient with the substrate and low thermal conductivity are of paramount importance, which motivates an in-depth investigation into the thermal properties of CrTa_0.5Nb_0.5O₄.

The aforementioned research findings demonstrate that CrTa_0.5Nb_0.5O₄ manifests remarkable advantages in mechanical properties and thermal conductivity. To fundamentally reveal the inherent mechanisms underlying its excellent performance and fully explore its potential application values, subsequent studies will focus on the atomic scale microstructure analysis. Through microscopic structural analysis, the influences of composition, atomic arrangement and other factors on its properties will be systematically investigated, which will provide more solid theoretical support for the optimized design and practical application of CrTa_0.5Nb_0.5O₄.

As illustrated in Fig. 5(a), the HAADF image of bulk CrTa_0.5Nb_0.5O₄ processed by FIB technology reveals distinct contrast phases, prompting energy-dispersive spectroscopy (EDS) for elemental characterization. Figs. 5(b)-5(e) display the corresponding elemental mappings of Cr,Ta, Nb, and O, while Fig. 5(f) presents the merged elemental distribution of these three transition metals (Cr,Ta,Nb ). Notable observations include: red rectangle region showing co-distribution of all four elements (Cr, Ta,Nb,O ); blue rectangle region featuring high Cr and Nb contents with trace Ta; green areas characterized by dominant Cr with negligible Ta and Nb. Intriguingly, although the XRD pattern in Fig. 2 exhibiting diffraction peaks exclusive to a single phase, the integrated analysis with Fig. 5 provides compelling evidence for the coexistence of three distinct phases within the bulk material. In accordance with the fundamental principle of stereology, which states that under random sampling conditions, the three-dimensional volume fraction of a given phase within a material is equivalent to its area fraction in two-dimensional cross-sectional images, we quantified the area distributions of the three phases using ImageJ software to determine their volume ratio. Subsequent calculations yielded an approximate volume ratio of CrTa_0.5Nb_0.5O₄,CrNbO₄, and CrO₂ to be 94.25%:2.41%:3.34%. To further determine the compositions and crystal structures of the three phases, atomic-scale high-resolution scanning transmission electron microscopy (HR-STEM) combined with EDS mapping analyses were performed on the respective regions highlighted in Fig. 5. Specifically, Fig. 6 presents the HAADF image acquired from the red rectangle region in Fig. 5(a), revealing atomic-column resolved contrast that facilitates direct structural interpretation. In HAADF-STEM image, the bright spots in the image can reflect the real atoms or atomic pairs, and the intensity of the image points is proportional to the square of the atomic number, while the ABF image contrast is proportional to one-third of the atomic number. Fig. 6(a) is the HAADF image of rutile structured CrTa_0.5Nb_0.5O₄ in [012] zone axis and the overlaid atomistic structure in the figure. Figs. 6(b)-6(e) are the EDS element mapping of Cr,Ta,Nb and O corresponding to the HAADF in Fig. 6(a). Fig. 6(f) is the HAADF image of rutile structured CrTa_0.5Nb_0.5O₄ in [101] zone axis and the overlaid atomistic structure in the figure. Figs. 6(g)-6(j) are the EDS element mapping of Cr,Ta,Nb and O corresponding to the HAADF in Fig. 6(f). Combining the analyses of Figs. 6(a) and Figs. 6(f), the atomic site occupation demonstrates a high degree of consistency with the rutile structure. By integrating the analyses from Fig. 6(a) and Fig. 6(f), the calculated unit cell parameters of CrTa_0.5Nb_0.5O₄ are determined to be a=4.646Å and c=3.018Å, which show close agreement with the results derived from XRD refinement in Fig. 1(d). Specifically, Cr, Ta, and Nb exhibit random occupation of the (0,0,0 ) lattice sites. Elemental area scanning results confirm that the elemental composition closely aligns with the designed molar ratio of Cr:Ta:Nb=2:1:1, strongly indicate that CrTa_0.5Nb_0.5O₄ is a rutile-structured solid solution. The grain boundary plays a crucial role in determining the mechanical and thermal properties of ceramics. From the HAADF image in Fig. 6(k), one finds that there is no amorphous layer at the interphase boundary, i.e., the interface between two grains is lattice-lattice directly matched. Figs. 6(l)-6(n) show the distributions of elements Cr,Nb, and Ta, respectively, while Fig. 6(o) is the merged mapping images of Cr, Ta,Nb and O. EDS line scanning (denoted by the purple line in Fig. 6(o)) was used to analyze the elemental distribution at the interface. It can be observed that Cr,Ta,Nb, and O are uniformly distributed near the interface without obvious enrichment or segregation phenomena, as can be seen from Fig. 6(p).

The presence of impurities exerts a non-negligible influence on the mechanical and thermal properties of bulk materials. Therefore, in-depth investigation and accurate determination of impurity composition and distribution in bulk materials are of significant importance. Further analysis was performed on the blue- rectangle region in Fig. 5, yielding the HAADF image shown in Fig. 7(a). Figs. 7(b)-7(d) present the elemental mappings of Cr,Nb, and O, respectively. Combined with the elemental distribution, the impurity phase in the blue region was identified as CrNbO₄ with a rutile-type crystal structure, and the calculated lattice parameter a is 4.648 A. Similarly, in-depth analyses of the elemental composition and crystal structure were conducted for the third phase. Figs. 7(e) and Figs. 7(f) show the HAADF and ABF images of the third phase, respectively, while Figs. 7(g) and Figs. 7(h) depict the elemental distributions of Cr and O. Based on the results from Figs. 7(e) to 7(h), the impurity phase in the red region was identified as rutile-structured CrO₂. Figs. 7(e) and Figs. 7(f) are the HAADF and ABF-STEM images of CrO₂ in [011] zone axis. The calculated lattice parameters are a=4.437Å and c=2.938Å, which are in good agreement with those reported in the literature [45]. Overall, three phases were identified in the bulk material: CrTa_0.5Nb_0.5O₄,CrNbO₄, and CrO₂. Due to their akin rutiletype crystal structures and highly similar unit cell parameters, these phases are indistinguishable in the XRD patterns presented in Figs. 1(a) and Figs. 2(a). Characterizing the composition and crystal structure of the impurity phases offers critical insights into the mechanisms underlying the observed enhancements in mechanical and thermal properties, which will be discussed in the next section.

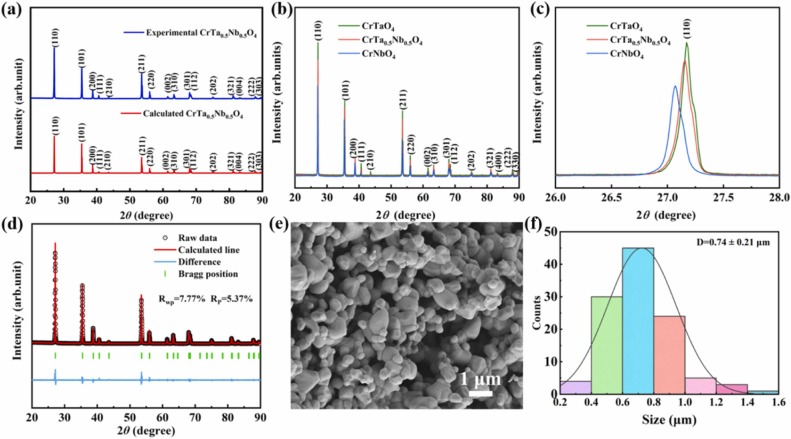
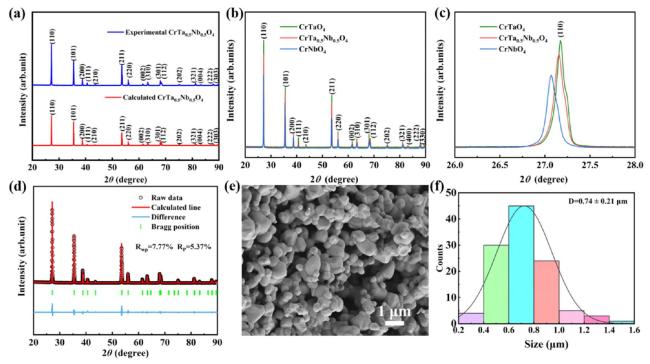
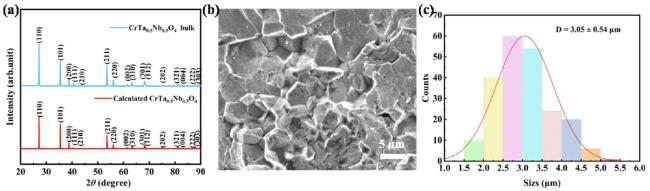
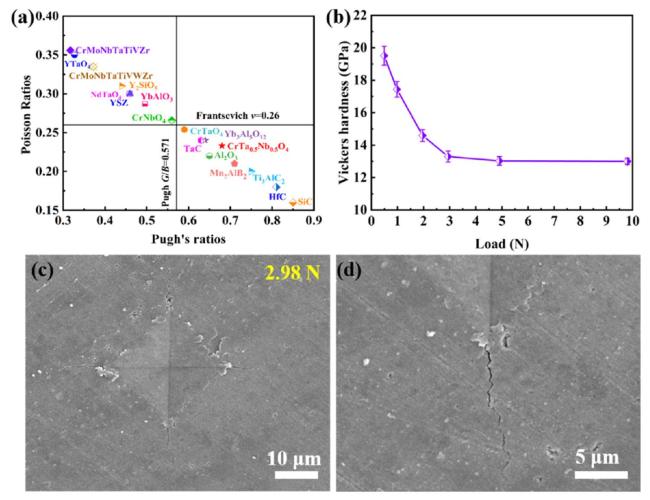
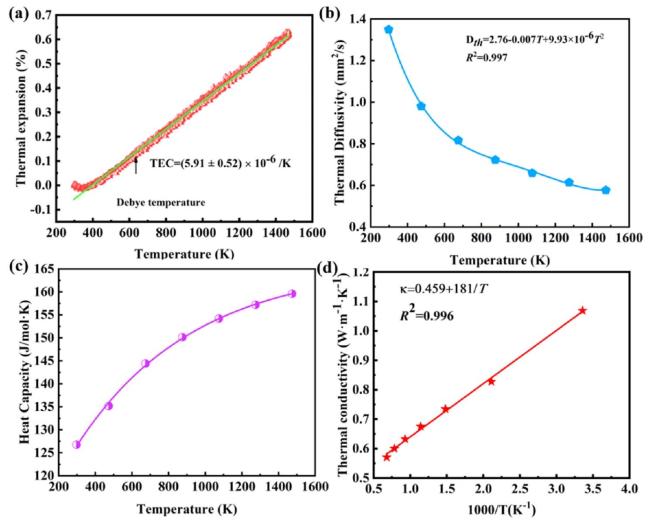
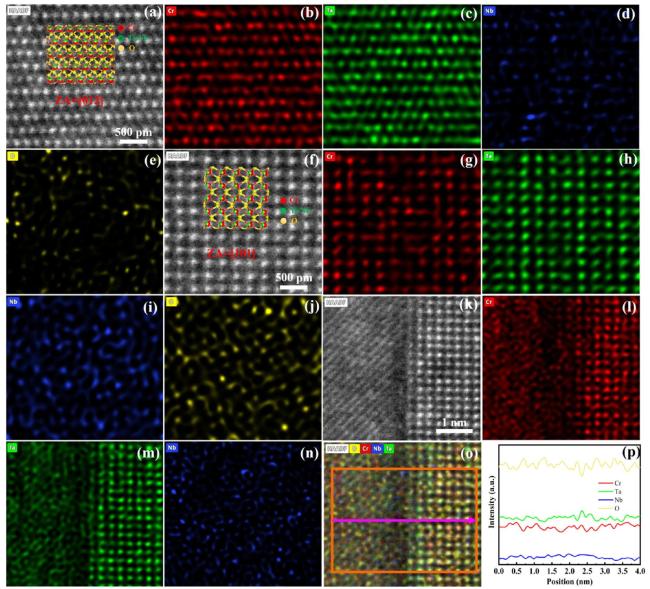
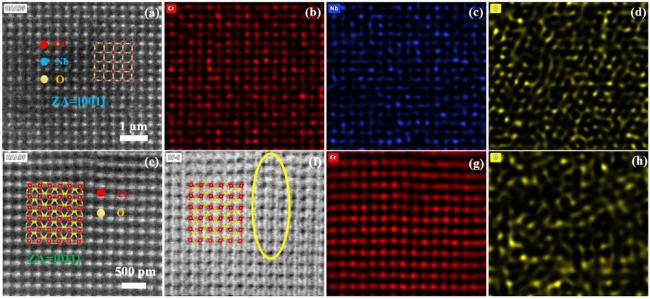
In terms of mechanical properties, the Vickers hardness of CrTa_0.5Nb_0.5O₄ is 13.01±0.20GPa, indicating a 6.6% increase compared to ${\mathrm{C}\mathrm{r}\mathrm{T}\mathrm{a}\mathrm{O}}_{4}\left(\right(12.20\pm 0.44\mathrm{G}\mathrm{P}\mathrm{a})$ and a 27.5% increase compared to CrNbO₄(10.20±0.58GPa). The fracture toughness of CrTa_0.5Nb_0.5O₄ is 2.07±0.017MPa⋅m¹/ ², representing a 10.7% increase over ${\mathrm{C}\mathrm{r}\mathrm{T}\mathrm{a}\mathrm{O}}_{4}\left(1.87\pm 0.074\mathrm{M}\mathrm{P}\mathrm{a}\cdot {\mathrm{m}}^{1}/{ }^{2}\right)$ and a 33.1% increase over ${\mathrm{C}\mathrm{r}\mathrm{N}\mathrm{b}\mathrm{O}}_{4}\left(1.54\pm 0.124\mathrm{M}\mathrm{P}\mathrm{a}\cdot {\mathrm{m}}^{1}/{ }^{2}\right)$. Based on microstructure analyses presented Fig. 5, it is proposed that the primary strengthening mechanisms are attributed to solid solution strengthening and dispersion strengthening. The solid solution strengthening in CrTa_0.5Nb_0.5O₄ is primarily attributed to lattice distortion induced by the differences in atomic radius and electronegativity among Cr,Nb, and Ta. The differences in atomic properties among Cr,Nb, and Ta constitute the core origin triggering solid-solution strengthening. On one hand, there exist significant distinctions in their ionic sizes: Cr³⁺ has a radius of approximately 0.62Å, while both Nb⁵⁺(≈0.69Å) and Ta⁵⁺(≈0.64Å) are larger than Cr³⁺. When Nb⁵⁺ and Ta⁵⁺ substitute for Cr³⁺ in the lattice, their larger ionic sizes force the surrounding lattice to undergo local tensile deformation, forming inhomogeneous strain fields. On the other hand, there is a charge difference of +3 versus +5 between Cr³⁺ and Nb⁵⁺/Ta⁵⁺. This charge imbalance induces perturbations in the local electrostatic field, further exacerbating lattice irregularities. The lattice strain fields resulting from size mismatch and the electrostatic perturbations caused by charge differences collectively form a "composite resistance field" that hinders dislocation motion. When the material undergoes plastic deformation under external forces, the migration of dislocations (as carriers of lattice slip) is subjected to mechanical obstruction from the strain fields. Meanwhile, electrostatic perturbations enhance the interaction energy between dislocations and surrounding ions. The superposition of these two effects means that dislocations must overcome a higher energy barrier to continue moving, ultimately manifesting as an improvement in the material's strength and hardness, thus achieving solid-solution strengthening. Additionally, the presence of impurity phases (CrNbO₄ and CrO₂ particles) in the CrTa_0.5Nb_0.5O₄ matrix exerts a dispersion strengthening effect. Dispersion strengthening enhances the material's resistance to deformation by means of second-phase particles such as fine impurity particles that impede dislocation motion. When the material undergoes plastic deformation under external force, dislocations need to traverse the impurity particles (i.e., CrNbO₄ and CrO₂ ) in the matrix. As dislocations propagate within the material, upon encountering CrNbO₄ and CrO₂ particles, they bend and loop around these particles to pass through. This process requires overcoming the line tension of the bent dislocations and consuming additional energy, which hinders the motion of dislocations. Consequently, the mechanical properties of the material, such as strength and hardness, are improved. The two mechanisms of solid-solution strengthening and dispersion strengthening can achieve the effects of "resistance superposition" and "spatial complementarity": the lattice distortion from solid-solution strengthening keeps dislocations in a state of continuous hindrance during long-distance movement, while the particle pinning from dispersion strengthening forms locally insurmountable obstacles. After dislocations break through the obstruction of the solid-solution stress field, they will soon encounter further interception by impurity particles. 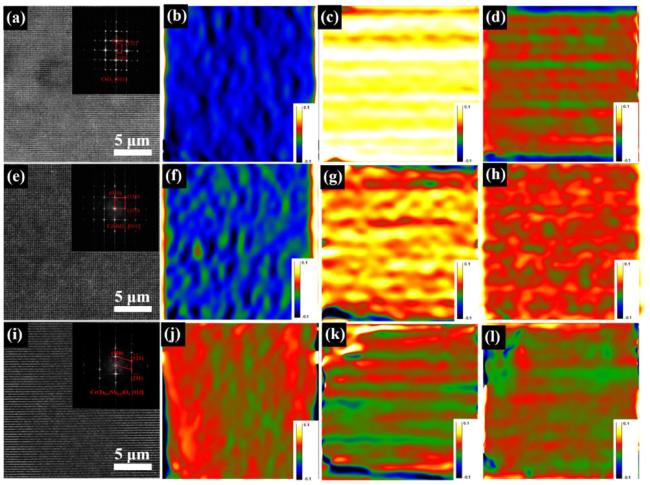Meanwhile, significant lattice distortions were observed in CrO₂ in Figs. 7(e) and Figs. 7(f), such as the areas marked by yellow circles. To characterize this phenomenon accurately, Geometric Phase Analysis (GPA) was employed for strain quantification, including quantitative studies on the distribution of CrO₂ along the [011] zone axis, as well as CrNbO₄ along the [001] zone axis and CrTa_0.5Nb_0.5O₄ along the [113] zone axis. GPA analyses reveal that the mapping of horizontal normal strain (ε_xx ), vertical normal strain (ε_yy ) and shear strain (ε_xy ) are randomly distributed. In the strain intensity color scale, white-blue pixels characterize regions of high strain, while red-green pixels correspond to states of low strain. The results in Fig. 8 demonstrate that the strains in CrO₂ and CrNbO₄ are significantly greater than those in CrTa_0.5Nb_0.5O₄. This implies that within the material, CrTa_0.5Nb_0.5O₄ is subjected to a compressive stress, while CrO₂ and CrNbO₄ experience tensile stresses. Upon the application of external stress, the compressive stress in the CrTa_0.5Nb_0.5O₄ matrix counteracts part of the load, thereby enhancing the material's hardness, strength and toughness.

In terms of thermal properties, the thermal conductivity of CrTa_0.5Nb_0.5O₄ at room temperature is 1.07Wm^-1⋅ K^-1, which is lower than that of ${\mathrm{C}\mathrm{r}\mathrm{T}\mathrm{a}\mathrm{O}}_{4}\left(1.31{\mathrm{W}\mathrm{m}}^{-1}\cdot {\text{ }\mathrm{K}}^{-1}\right),{\mathrm{C}\mathrm{r}\mathrm{N}\mathrm{b}\mathrm{O}}_{4}\left(1.09{\mathrm{W}\mathrm{m}}^{-1}\cdot {\text{ }\mathrm{K}}^{-1}\right)$. The reduction in thermal conductivity can be analyzed from the following aspects. Firstly, the configurational entropy ( ${S}_{\text{config}\text{ }}=-R\left(\sum _{i=1}^{N}  {x}_{i}\mathrm{l}\mathrm{n}{x}_{i}\right)$ ) [46] of CrTaO₄ and CrNbO₄ is 0.69R, whereas that of CrTa_0.5Nb_0.5O₄ reaches 1.04R. The enhanced configurational entropy in CrTa_0.5Nb_0.5O₄ gives rise to more pronounced atomic radius mismatches and charge fluctuations among cations (Cr³⁺,Ta⁵⁺,Nb⁵⁺ ), thereby inducing lattice strains and local distortions. Such structural perturbations exacerbate phonon scattering, leading to a consequent reduction in thermal conductivity. Additionally, besides the matrix phase CrTa_0.5Nb_0.5O₄, the impurity phases of CrNbO₄ and CrO₂ are present. Although the three phases share the same type of crystal structure, differences in elastic properties cause phonons to change propagation directions during scattering, thereby hindering heat conduction and thus reducing thermal conductivity. Furthermore, as shown in Fig. 8, significant residual strain exists in CrO₂, which distorts the lattice and disrupts crystal symmetry, which increases the probability of phonon scattering and further reduces the thermal conductivity of CrTa_0.5Nb_0.5O₄.

CrTa_0.5Nb_0.5O₄ demonstrates an elevated melting point (2073 K) and exhibits good thermal stability. Intriguingly, its mechanical properties closely mirror those of YSZ, while maintaining a significantly low thermal conductivity. These findings inspire speculation on the potential of CrTa_0.5Nb_0.5O₄ as a novel thermal barrier coating (TBC) material, positioning it comparably to CrTaO₄ and CrNbO₄. From the dual perspectives of TBC functional performance and system-level compatibility, the following attributes are critical for an ideal TBC material [47,48]: (1) ultralow thermal conductivity to minimize heat transfer; (2) a thermal expansion coefficient that closely matches the substrate, ensuring thermal stress mitigation; (3) robust corrosion resistance against harsh environmental conditions; (4) outstanding high-temperature stability to withstand prolonged exposure at elevated temperatures; (5) a high melting point to prevent phase degradation; and (6) superior mechanical properties, enabling resistance to mechanical stresses during operation. Consequently, the discussion will primarily focus on the thermal expansion coefficient and thermal conductivity. The TECs, room temperature thermal conductivities, and Young's modulus of common TBCs were plotted in a 3D graph, as depicted in Fig. 9. From Fig. 9, it is noteworthy that the TEC of CrTa_0.5Nb_0.5O₄ is much lower than that of currently investigated TBC materials, such as CrTaO₄(6.12×10^-6 K^-1) [8], CrNbO₄(5.84×10^-6 K^-1) [9], YSZ (10.5×10^-6 K^-1) [10], La₂Hf₂O₇(8.76×10^-6 K^-1) [49], Yb₃Al₅O₁₂(8.22×10^-6 K^-1) [32], La₂Zr₂O₇(9×10^-6 K^-1) [50] but higher than that of γ-Y₂Si₂O₇(3.9×10^-6 K^-1) [51]. Of particular interest, the TEC of CrTa_0.5Nb_0.5O₄ is close to those of refractory alloys such as Ta (6.3×10^-6 K^-1 ) and Nb(7.3×10^-6 K^-1) [11] and UHTCs such as HfB₂(6.3×10^-6 K^-1) [52], TaC(6.6×10^-6 K^-1), and NbC (6.8×10^-6 K^-1 ) [12]. Therefore, from the perspective of matched TECs, CrTa_0.5Nb_0.5O₄ is promising as protective TBC for refractory metals such as Ta and Nb and their alloys as well as UHTCs or as a protective scale to prevent the further oxidation of these materials once it forms on their surfaces upon oxidation. For thermal barrier applications, low thermal conductivity in the application temperatures is another important gauge to judge the suitability of a candidate material. The thermal conductivity of CrTa_0.5Nb_0.5O₄ is much lower than that of some common TBC such as CrTaO₄ [8], CrNbO₄ [9], YSZ [10], β Lu₂Si₂O₇ [53], γ-Y₂Si₂O₇ [51], Y₂SiO₅ [29], La₂Zr₂O₇ [50], Yb₃Al₅O₁₂ [32], La₂Hf₂O₇ [49], TiO₂ [40], and ErTaO₄ [36]. Considering the comprehensive mechanical properties, thermal expansion coefficient, and thermal conductivity, CrTa_0.5Nb_0.5O₄ is considered promising as a thermal barrier coating material for RM, RHEAs, UHTCs and other materials.