Extreme Materials

Figure/Table detail

Recent Advances in High-entropy Ceramics: Design Principles, Structural Characteristics, and Emerging Properties

Yiran Li, Donghui Pan, Jiehui Cao, Wenhui Fang, Yiwang Bao, Bin Liu

Extreme Materials, DOI: 10.1016/j.exm.2025.05.002

Symbol	Name	Definitional Formula	Physical Meaning		Ref
ΔS_mix	Mixed entropy	$\Delta S_{mix}=−R_{i}\sum c_{i}lnc_{i}$	c_i is the content of different components.		[71]
ΔH_mix	Enthalpy of mixing	$ΔH_{mix}=E_{HEC}-\sum c_{i}E_{i}$	The sum of the interaction energy differences in the ideal state.		[72]
Ω	Entropy-enthalpy balance factor	$Ω=\frac{T_{m}\Delta S_{mix}}{\|\Delta H_{mix}\|}$	Tₘ is the isothermal temperature.		[73]
δ	Atomic (ion) radius difference	$δ=\sqrt{\sum_{i}c_{i}(1-\frac{r_{i}}{\overline{r}})^2}, \overline{r}=\sum_{i}c_{i}r_{i}$	Contribution of differences in atomic/ionic radii of components to lattice distortion		[74]
Δχ	Electronegativity difference	$\Delta\chi =\sqrt{\sum_{i}c_{i}(\chi_{i}-\overline{\chi})^2}$, $\overline{\chi}=\sum_{i}c_{i}\chi_{i}$	Δχ reflects the difference in electronegativity between different elements.		[75]
VEC	Valence electron concentration	$VEC=\sum_{i}(valence\quad electrons \quad of \quad i)$	Reflects the degree of electron filling and energy band structure characteristics of the system		[74]
DEED	Disordered Enthalpy-Entropy Descriptor	$DEED=\sqrt{\frac{\sigma_{\Omega}^{-1} [H_{f}]}{<\Delta H_{hull}>_\Omega}}$	Predicting the possibility of single-phase disordered structures in multicomponent systems, H_f and Hf_ull are the DFT formation energies of the partial occupation POCC tiles and the convex hull, respectively.		[76]
EFA	Entropy forming ability	$EFA=(\sqrt{\frac{\sum_{i=1}^{n}g_{i}(H_{i}-H_{mix})^2} {\sum_{i=1}^{n}g_{i}-1}})^{-1}$	Entropy-driven formation of stable single-phase solid solutions, where n is the total number of sampled geometrical configurations and g_iare their degeneracies. H_i of the sampled configurations.		[66]
LDI	lattice distortion index	$LDI=\sum_{i=1}^{n}\sqrt{(x_{i,a}-x_{i,0})^{2}+(y_{i,a}-y_{i,0})^{2}+(z_{i,a}-z_{i,0})^{2}/n}$		Parameters for the degree of lattice distortion in disordered systems, (x, y) is the atomic position.	[77]
$γ$	The normalized geometric packing parameter for the metallic sublattice calculated	$\gamma =(1-\sqrt{1-\frac{(r_{s}+\overline{r})^{2}-\overline{r}^2}{(r_{s}+\overline{r})^2}})/(1-\sqrt{1-\frac{(r_{L}+\overline{r})^{2}-\overline{r}^2}{(r_{L}+\overline{r})^2}})$		Evaluating how different metal atoms stack together in a crystal lattice, where r_s and r_L are the radii of the smallest and largest atoms.	[78]

Table 1. Parameters and Descriptors Related to Theoretical Design

Other figure/table from this article

Fig. 1. (b) All the constituent elements reported in HECs to date. (b) Total number of publications on major HECs over the last decade. Data was retrieved from Web of Science on February 28, 2025, using keywords: “high-entropy”, “oxide”, “boride”, “carbide”, “nitride”, “silicide”, “fluoride”, “hydride”, “phosphide”, “sulfide”, and “ceramics”.
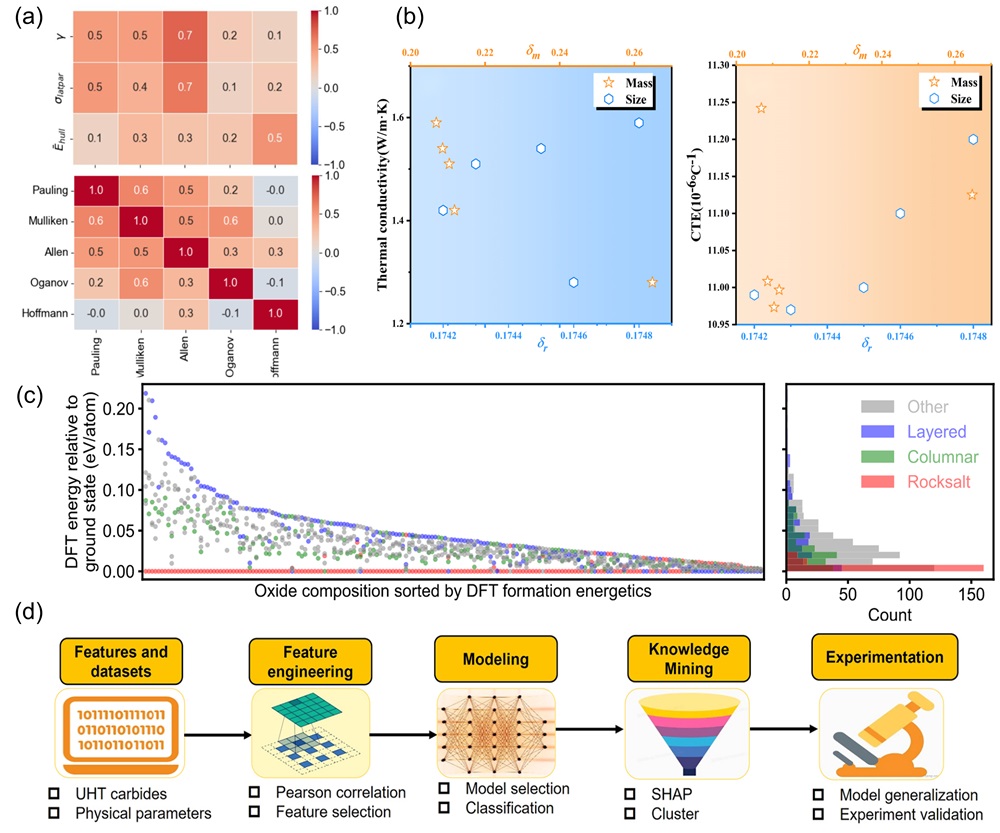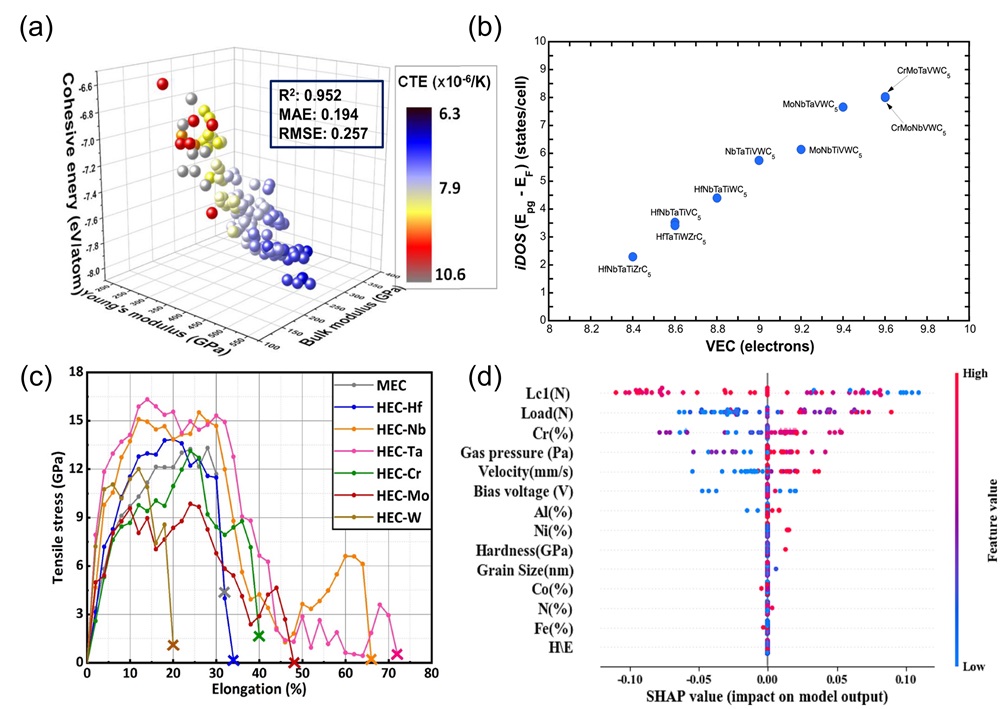Fig. 2. (a) Pairwise correlations of computational parameters: atomic radius deviations, lattice parameters, stabilization factors for miscible binary carbides, and electrochemical factors on different scales (top); correlations between different electronegativity scales (bottom) [64]. (b) Atomic size difference and atomic mass difference vs. thermal conductivity (left) and thermal expansion coefficient (right) at 1100°C [67]. (c) DFT (Density Functional Theory)-computed formation energies of the six model cation arrangements relative to the DFT-derived ground-state cation arrangement (left); oxide compositions are sorted in descending order of the highest DFT-computed formation energy relative to the ground state (right) [60]. (d) Workflow of machine learning for HECs. [68].
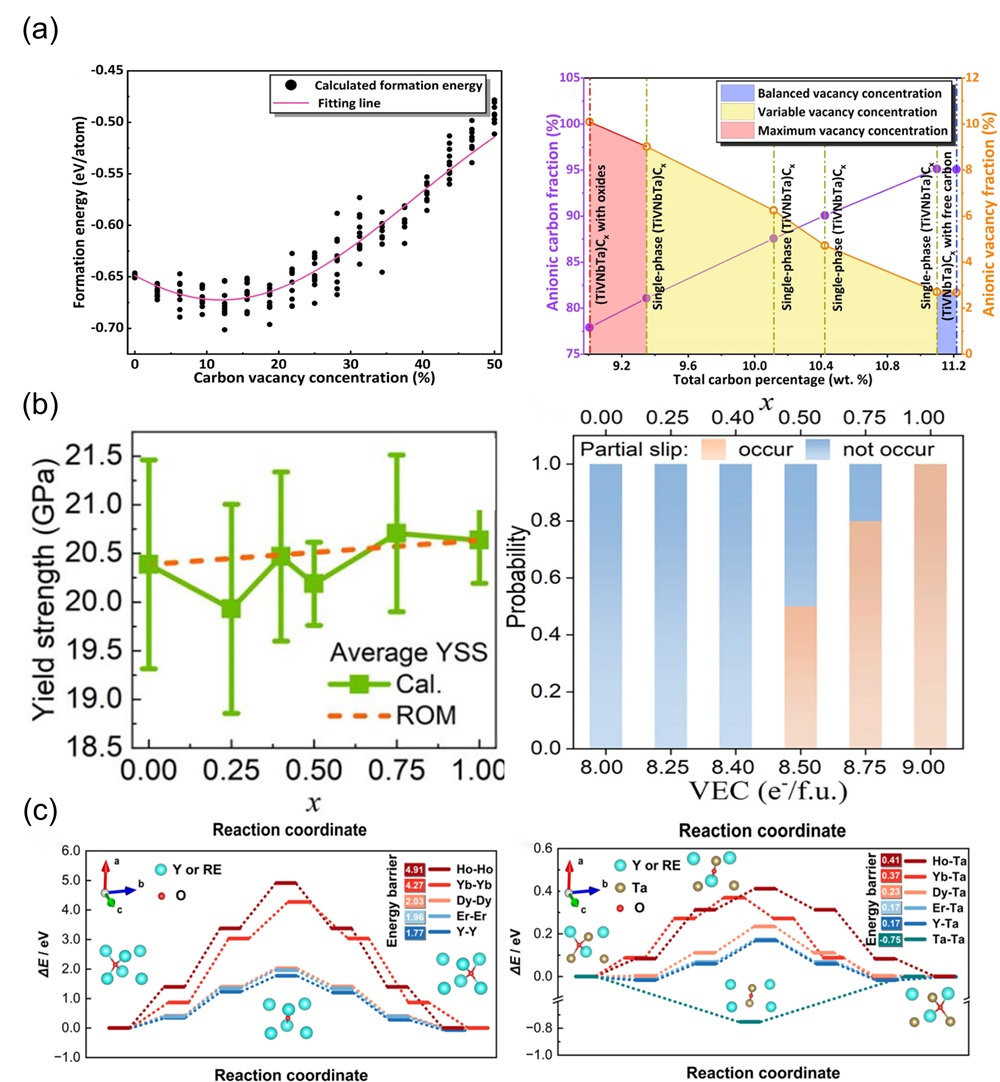Fig. 3. (a) The 3D plots of the NET (neural network) training set were generated based on three parameters (bulk modulus, Young's modulus, and cohesive energy) [79]. (b) A plot of (iDOS(E_pg, E_F)) vs. VEC composed of nine solid solution high-entropy carbides shows that iDOS increases linearly along with VEC, and Pearson's correlation coefficient was 0.99 [82]. (c) The stress-strain curves from the AIMD (Ab Initio Molecular Dynamics) tensile simulations of MEC and HEC [77]. (d) SHAP (Shapley Additive exPlanations) visualization features importance ranking [84].
Fig. 4. (a) The fitting formation energy curve of (TiVNbTa)C_x with variation of anionic vacancy concentration; Curves of anionic carbon and vacancy fraction under changing carbon content [86]. (b) Average YSSs and ROM (rule of mixture) predictions for (HfTiZr)_1-_x (NbTa)_xC (left); for each x/VEC (valence electron concentration) value, whether partial slip occurs when shearing along the [1 $1 ¯$ 0](111) direction in five supercells with different atomic distributions (right) [89]. (c) Diffusion energy barriers for oxygen ions on the RE-RE edge (left) and on the RE-Ta and Ta-Ta edges (right), respectively, in RE₃TaO₇ [91].
Fig. 5. Typical crystal structures of high-entropy ceramics. Here, two color schemes are used to clarify the difference between simple and complex oxides, and 2×2×2 supercells for the three crystal structures at left side for better comparison.
Table 2. Synthesis methods for high-entropy simple oxides corresponding product features.
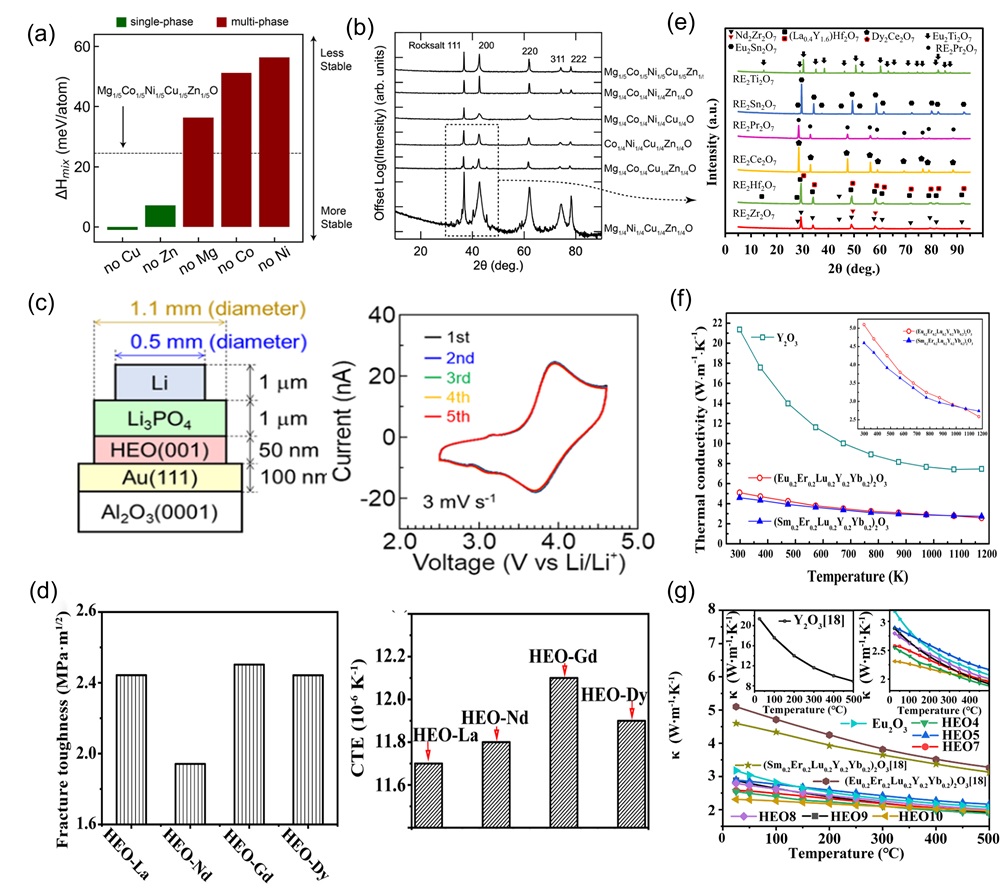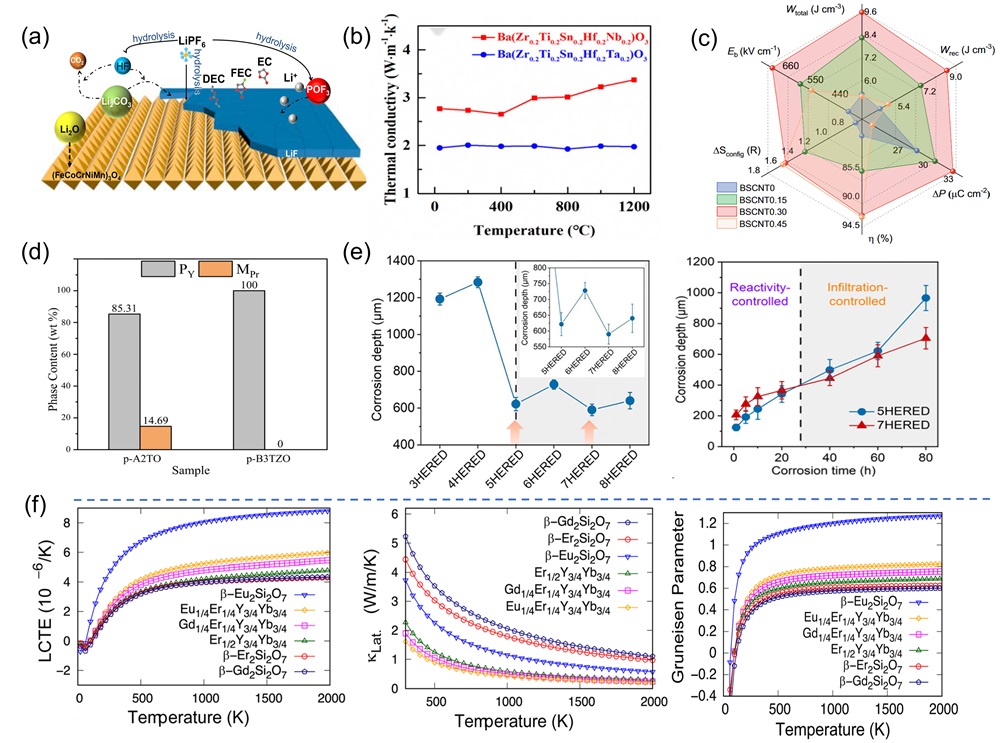Fig. 6. (a) X-ray diffractograms of four-component derivatives of (MgCoNiCuZn)O as a substrate; (b) DFT analysis of four diffractive phase compositions by mixing enthalpy [94]. (c) Side diagram of thin film battery with 50 nm Li(CrMnFeCoNiCu)O₂ (001) as positive electrode, and cyclic voltammogram [95]. (d) CTE and Fracture toughness of HEO-La, Nd, Gd, Dy [97]. (e) the XRD patterns of the samples. It can be seen that RE₂Zr₂O₇ and RE₂Hf₂O₇ failed to form single-phase high-entropy pyrochlore phase; RE₂Ce₂O₇ and RE₂Pr₂O₇ HEOs, exhibited a single phase structure with a fluorite-type structure [99]. (f) Calculation of thermal conductivity of (EuErLuYYb)₂O₃, (SmErLuYYb)₂O₃ and Y₂O₃ [105]. (g) Thermal conductivity κ curve of HEO4, 5, 7-10 and Eu₂O₃ [104].
Table 3. Synthesis methods for high-entropy complex oxides corresponding product features.
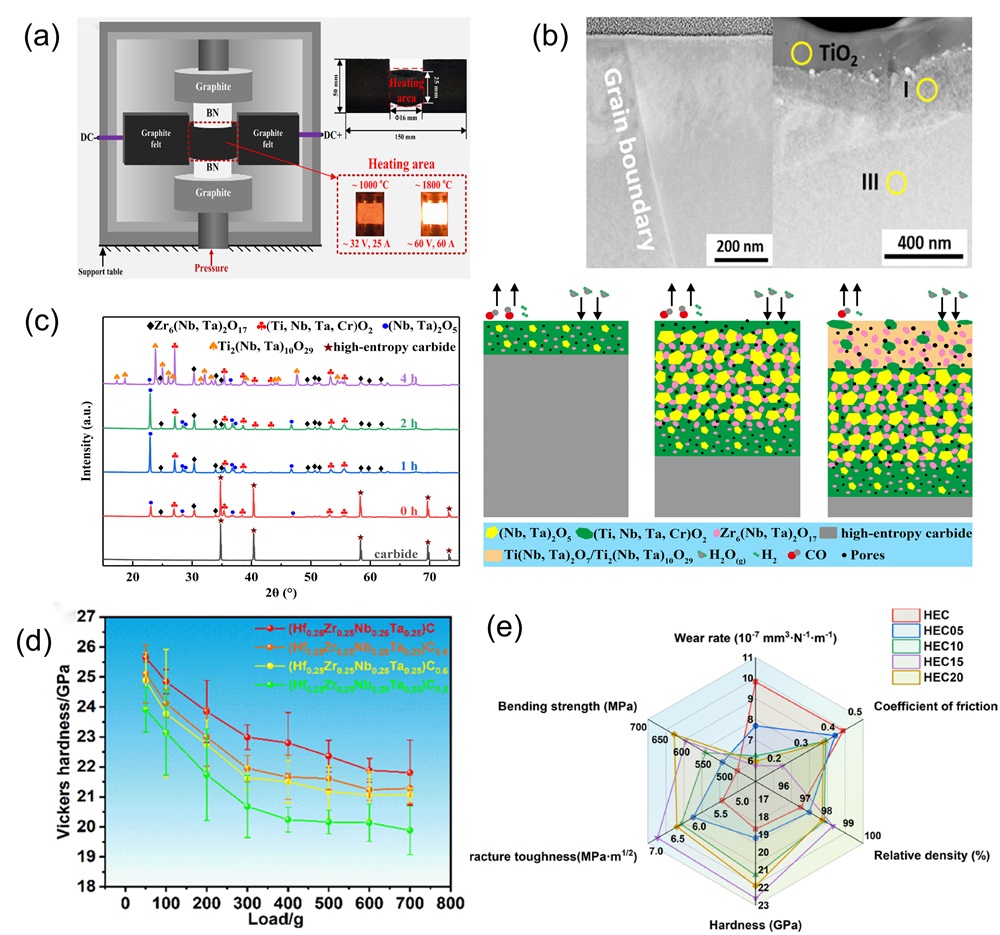Fig. 7. (a) Schematic diagram representation of the conversion of Li₂O, LiF, and Li₂CO₃ during the cycling process of the preconditioned HEOs [112]. (b) Comparison of thermal properties at X = Ta, Nb [117]. (c) Effect of different configurational entropy (different x) on energy storage performance [120]. (d) Effect of the introduction of Zr⁴⁺ on the content of the pyrochlore phase (PY) and monoclinic phase (MPr) [137]. (e) Corrosion depths of different component HEREDs at 1673K, 60 h; time-dependent curves of corrosion depths of 5HERED vs. 7HERED at 1673K [121]. (f) Thermal conductivity, CTE, and Grüneisen parameters as a function of temperature [140].
Table 4. Synthesis methods for high-entropy non-oxides corresponding product features.
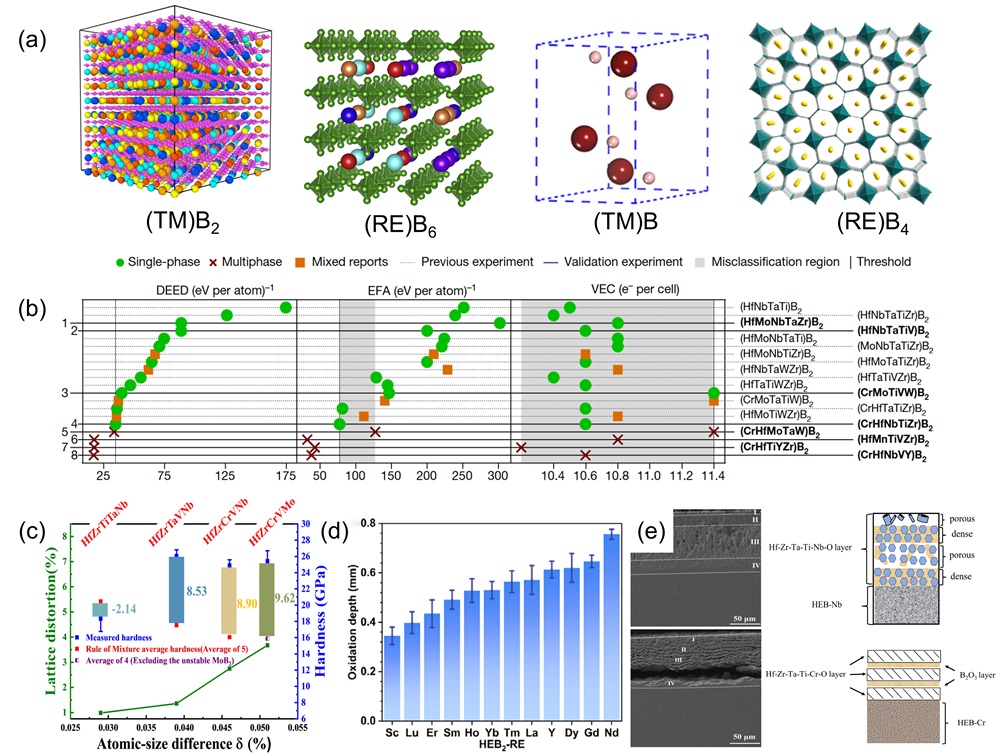Fig. 8. (a) Schematic diagram of ultra-fast pressure sintering apparatus [149]. (b) TEM cross-sections of the two samples sintered by SPS and SLS respectively, the sample with SPS has a uniform morphology and the sample sintered by SLS has a three-layer structure [148]. (c) XRD patterns of the samples oxidized for different durations, and Ti₂(Nb, Ta)₁₀O₂₉ appeared at 4 h; The schematic diagram of the oxidation mechanism of (TiZrNbTaCr)C in steam at 120°C [147]. (d) The function of H_v of sample sintered with applied loads [159]. (e) Comparison of various properties mechanical properties of HEC-SiCw with different C content [162].
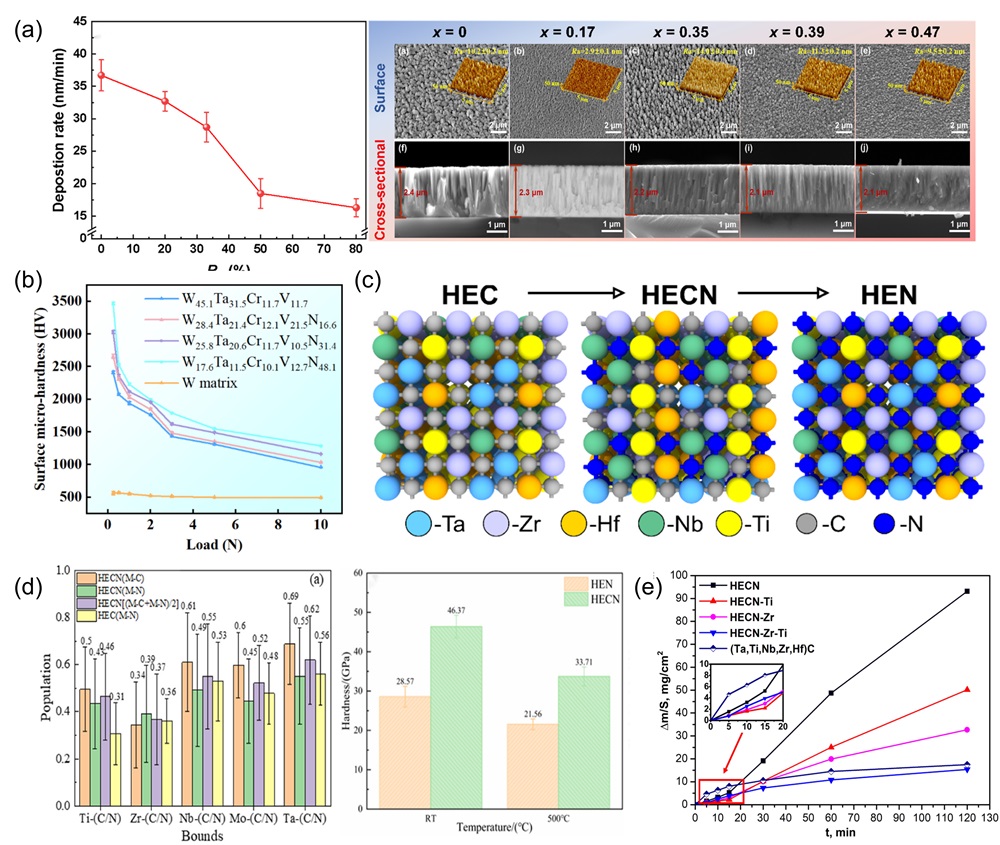Fig. 9. (a) Crystal structures of different HEBs [167] [170] [171] [172]. (b) Prediction of multiple HEB₂ syntheses by DEED: Compared with the results of EFA and VEC, the prediction of DEED was significantly better than the other two [10]. (c) Correlation between hardness, lattice distortion, and Atomic-size difference δ of HEB ceramics [164]. (d) Oxidation depth of twelve samples oxidized at 1673 K for 2h [145]. (e) HEB₂-Nd sample's oxide layer consists of a porous-dense-porous-dense four-layer structure; the oxide layer of the HEB₂-Cr sample exhibits a distinct layer structure [166].
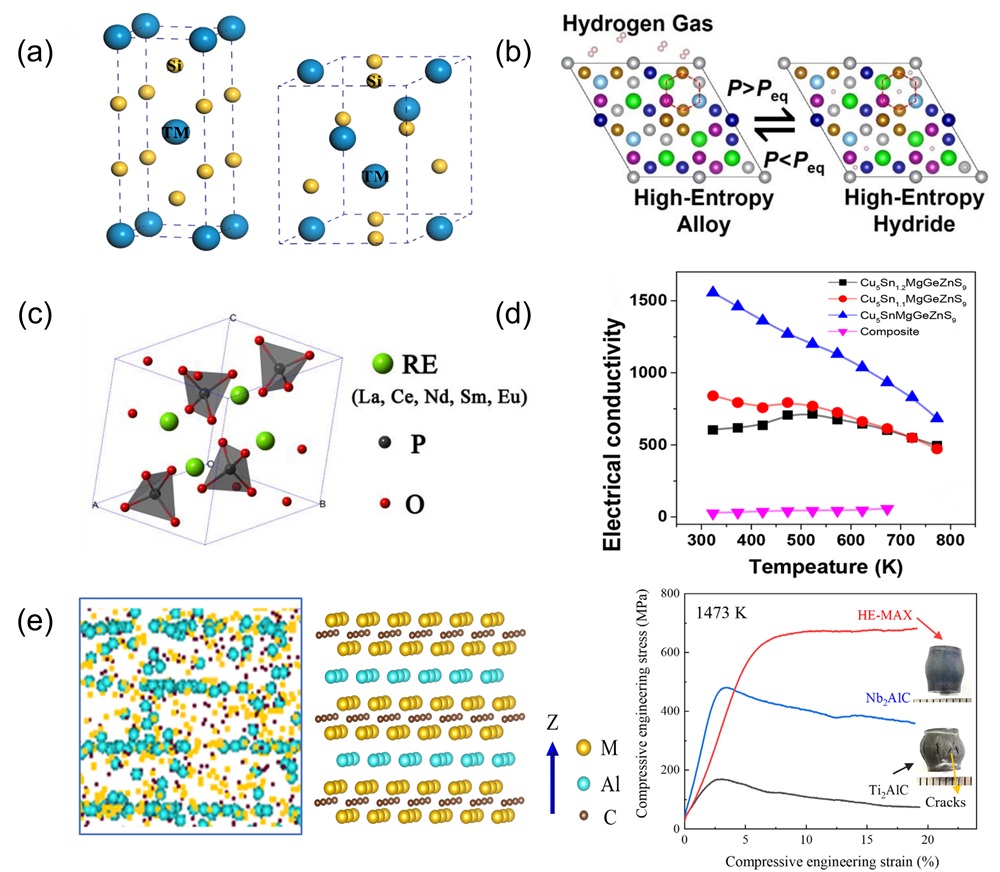Fig. 10. (a) SEM images of surface and cross-sectional morphology of (MoNbTaTiZr)_1-_xN_x coatings under different x; Deposition rates of (MoNbTaTiZr)_1-_xN_x coatings with different RN [177]. (b) Surface micro-hardness of W-Ta-Cr-V-N coatings [176]. (c) Crystal Structures of HEC, HECN, and HEN [174]. (d) Bond populations and density of states for HEN and HECN coatings; Crystal Structures of HEC, HECN, and HEN [179]. (e) The increase in mass per unit area as a function of oxidation time reflects the variation of the surface mass of the sample with time at different oxidation durations [54].
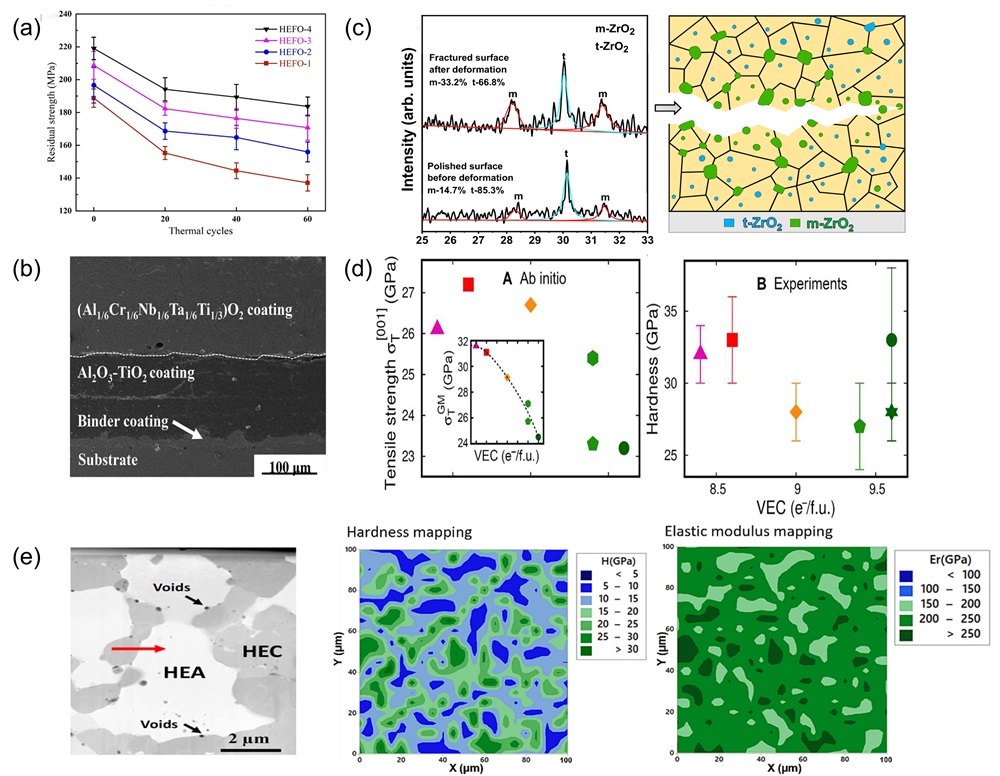Fig. 11. (a) Crystal structure of tetragonal transition metal disilicide (left), hexagonal transition metal disilicides (right) [196]. (b) Reversible phase transitions of HEA and HEH during hydrogen absorption [190]. (c) Crystal structure of HEPO₄ monazites [191]. (d) Electrical conductivity of the high-entropy sulfides [192]. (e) A tomogram slices of the HE-MAX phase lattice structure as well as a picture of the crystal structure in the ideal case; Compressive stress-strain curves of the HE-MAX, Nb₂AlC, and Ti₂AlC at 1473K, insets show the specimens after testing is completed [151].
Table 5. Summary of properties of high-entropy ceramics.
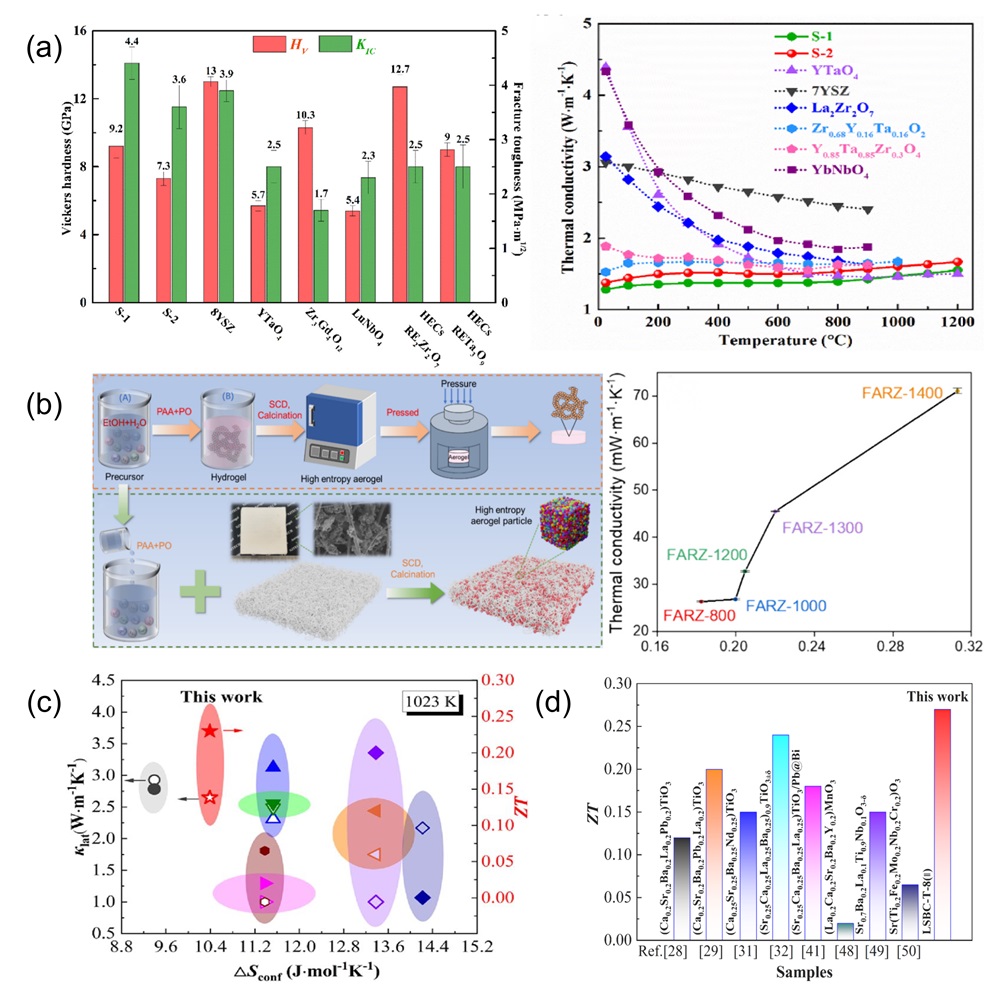Fig. 12. (a) Residual flexural strength after cyclic thermal shock at 1500℃ [200]. (b) The cross-section morphology of the ((AlCrNbTa)₂Ti)O₂ coating [197]. (c) (WTaNbZrTi)C before and after the application of pressure t-ZrO₂ and m-ZrO₂ content changes, and the martensitic phase transition of ZrO₂ under pressure schematic diagram, after the application of pressure the content of t-ZrO₂ is significantly reduced, and the content of m-ZrO₂ is increased accordingly [14]. (d) Comparison of the dependence of ideal tensile strength and nanoindentation hardness on VEC. The inset in A shows the geometric mean of the strain tensile strength recorded along [001] and [99] as a function of VEC [220]. (e) Mapping of nanohardness and elastic modulus in HEA₅₀C [13].
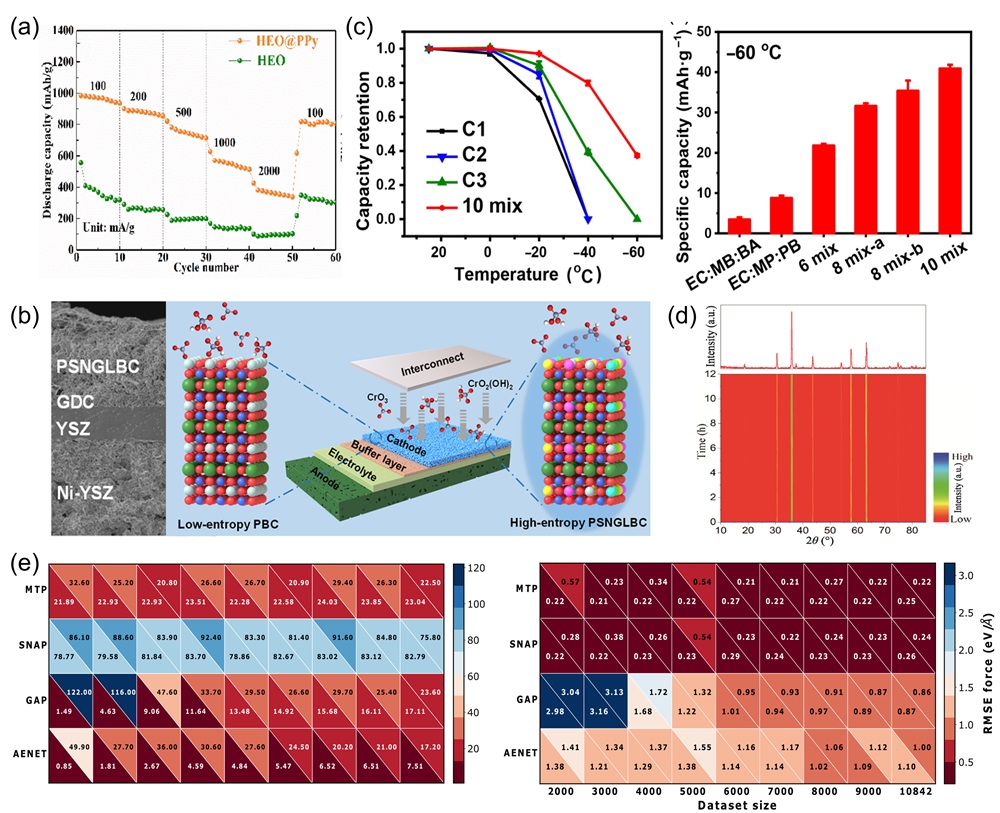Fig. 13. (a) Mechanical property comparisons between dual-phase zirconate/tantalate HECs, 8YSZ, YTaO₄, and others [204]. (b) The fabrication process of (YErYbGdLa)₂Zr₂O₇ ceramic aerogel and its thermal insulating properties [52]. (c) Comparison of PF (power factor) and ZT of ceramics with reported high-entropy perovskites at x = 0.10 [202]. (d) Comparison of the ZT in this study with those of previously reported high-entropy perovskites [203].
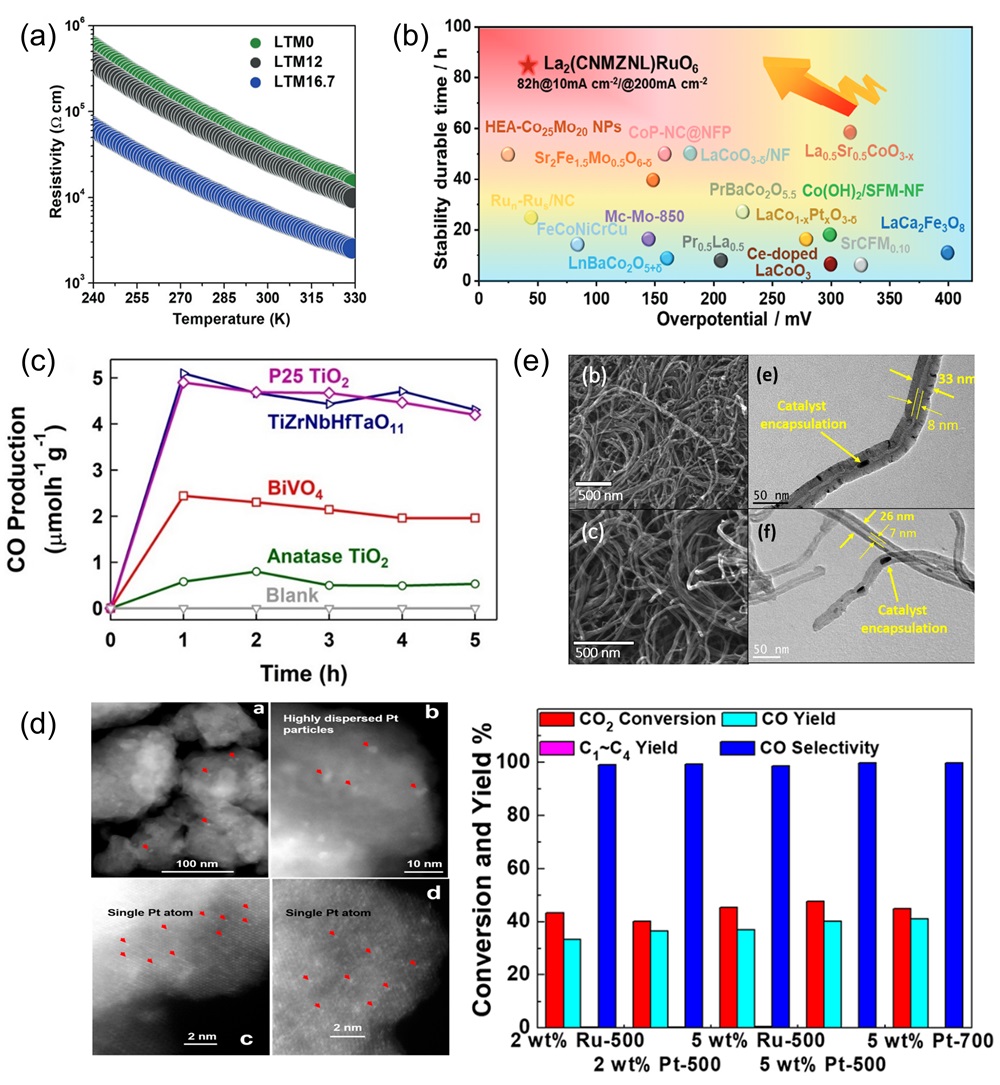Fig. 14. (a) The rate discharge performance of HEO and HEO@PPy at various current densities; the rate performance of HEO@PPy significantly outperforms that of HEO [224]. (b) Schematic and SEM cross-section of a single cell with (PrSmNdGdLa)BaCo₂O₅₊_δ cathode [206]. (c) Capacity retention of batteries utilizing commercial and decimal solvent-based electrolytes; comparison of capacity retention at -60°C for batteries with electrolytes comprising different solvent combinations [225]. (d) In situ XRD measurements of (FeMnCoNiCr)₃O₄ powder at 600℃ under a CO₂-containing atmosphere as a function of time (e) The MLIP energy (left panel) and force (right panel) of minimizing the root mean squared errors (RMSE). The lower-left and upper-right triangles within each square correspond to the training and test errors, respectively [226]. [33].
Fig. 15. (a) Temperature-dependent (ρ-T) electrical resistivity test [20]. (b) Overpotential and the stability durable time of La₂(CNMZNL)RuO₆ [21].(c) CO production rate versus time [22]. (d) Highly dispersed Pt particles (size range 2-3 nm) on HEO particles (right), and CO₂ hydrogenation activity (left) [230]. (e) FE (Field Emission)-SEM images of HEO-CNT and rHEO-CNT surface morphologies [231].
Fig. 16. (a) Magnetic induction strength versus temperature for (a-b) LC, (c-d) LCM, (e-f) LCMF, (g-h) LCMFA, and (i-j) LCMFAG ceramics in ZFC (Zero Field Cooling) and FC (Field Cooling) modes at 100 Oe and 1000 Oe, inset show the χ^-1 vs T and the straight line represents the C-W fitting [34]. (b) Hysteresis loops of the prepared HEOs at 300 K. The inset shows the low-field region of the hysteresis loops [122]. (c) Magnetization versus magnetic field curves for the samples at 25°C [131].
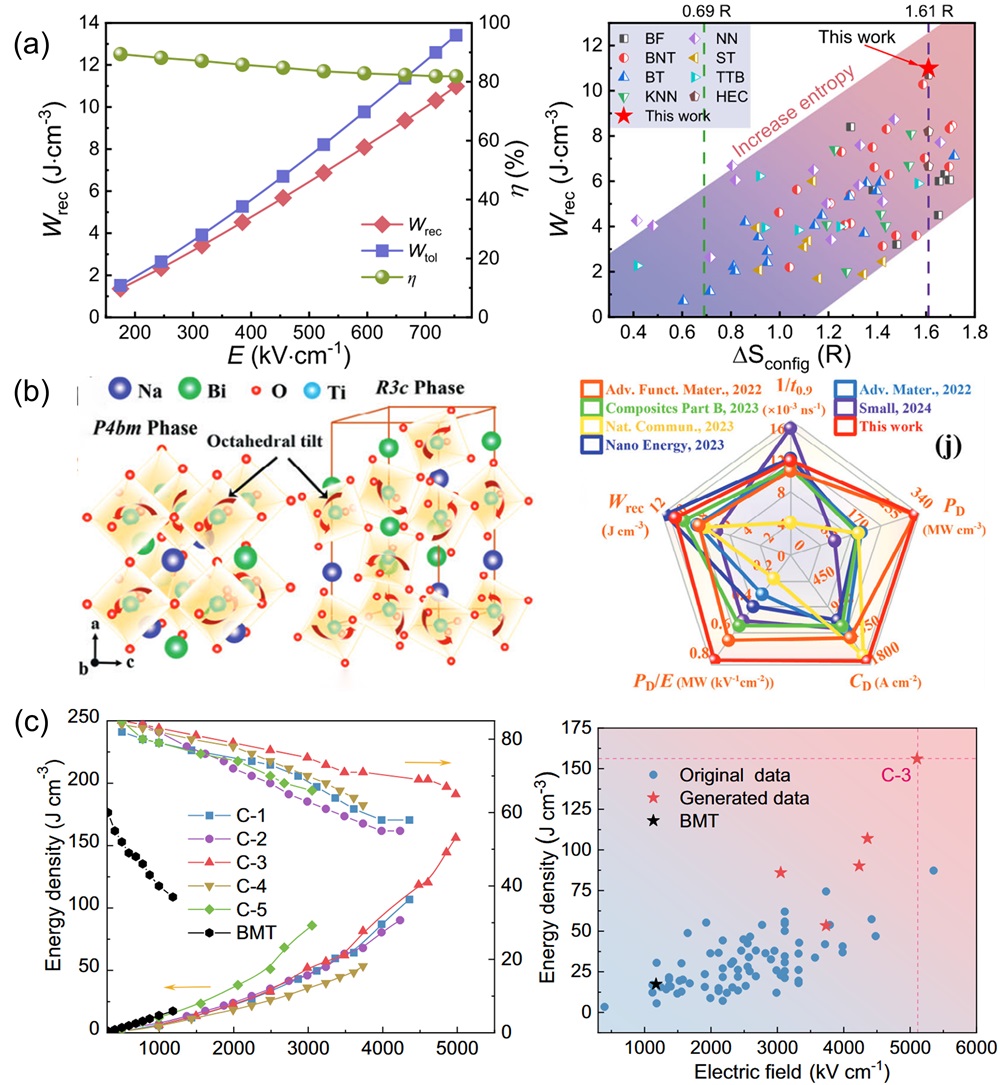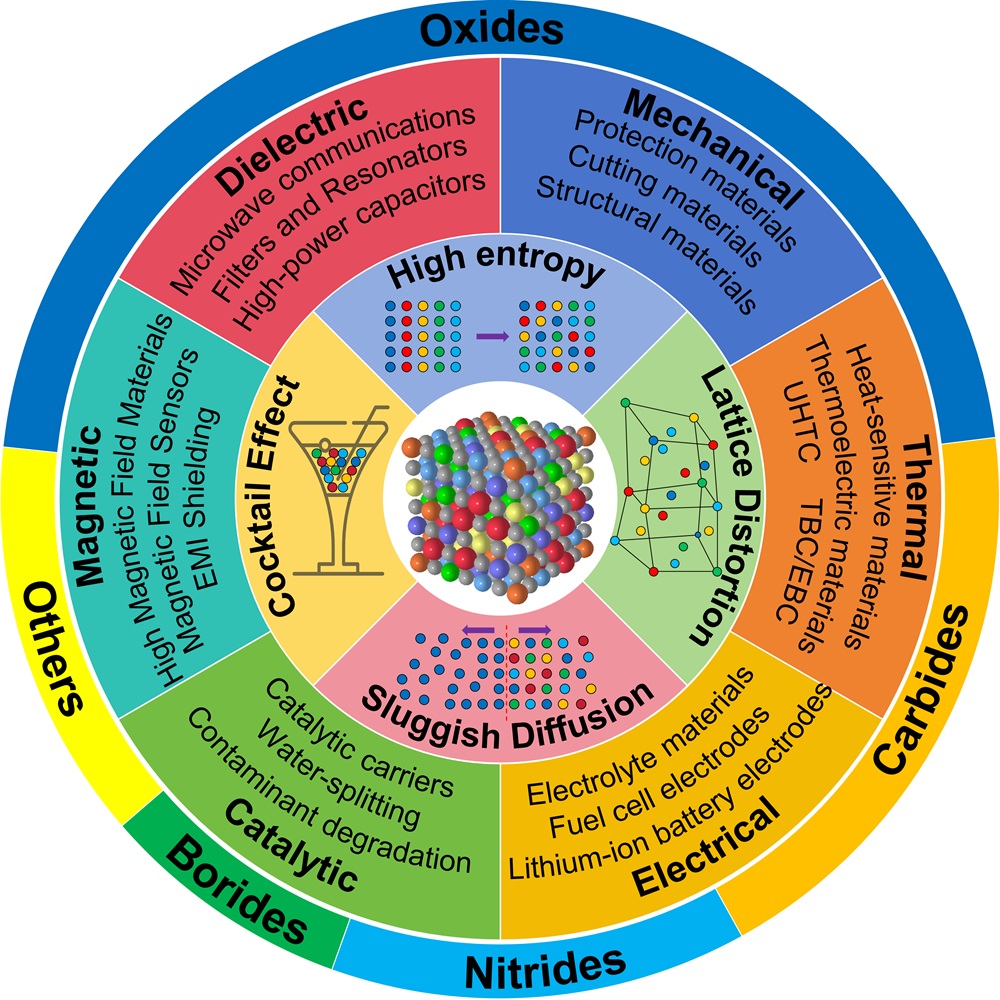Fig. 17. (a): W_rec and η as a function of electric field and W_rec comparison of (SrBaPbLaNa)Nb₂O₆ with other entropic materials of different configurations [36]. (b) Crystal structures of the R (R3c) and T (P4bm) phases with octahedral tilt; The overall energy storage performance of the obtained dielectric ceramics is compared with other work reported [216]. (c) Comparison of energy density and energy storage efficiency of generative learning screened compositions with pristine matrix Bi(Mg_0.5Ti_0.5)O₃ at different breakdown fields. Comparison of energy densities and breakdown fields between original experimental compositions, screened compositions, and the original matrix Bi(Mg_0.5Ti_0.5)O₃ [234].
Fig. 18. An overview diagram of HECs. The outer ring shows the percentage of studies on high-entropy oxides, carbides, nitrides, borides and others. The inner rings show the main applications of HECs, as well as the four core effects of high-entropy materials and a schematic of the disordered structure, respectively.